책 [Do it! 알고리즘 코딩 테스트 - 자바 편;김종관 지음]을 참고하여 작성하였습니다.
오일러 피 함수 P[N]
- 코딩 테스트에 자주 나오지는 않으나 알고 있어야 보임
- 1부터 N까지 범위에서 N과 서로소인 자연수의 개수
- 원리는 에라토스테네스('배수를 제거한다'는 원리)와 비슷
- 다른 점은 현재 배열의 값이 소수일 때, 그 배수를 제거하기 위해 배열의 끝까지 P[i] = P[i] - (P[i] / K) 연산을 수행한다는 것
(K는 현재 선택된 수, i는 K의 배수) - 이 과정은 N에서 해당 소인수 K의 배수를 제거하고 남은 수의 개수를 반영한다
실제 구현할 때는 N까지를 배열로 구현하지 않아도 되는데, 1부터 N까지의 서로소 개수를 result 변수로 생각하는 것이다. 그래서 처음에 N을 넣고 K를 2부터 시작해 N의 제곱근까지 같거나 작을 동안 배수를 지워 나간다. K가 N의 약수일 동안만 탐색하면 되니까 조건문을 걸고 아까의 P[i] = P[i] - (P[i] / K) 연산을 수행한다. 위에서 말했듯 result는 서로소의 개수를 담는 변수라는 것을 생각할 때 이 과정은 K의 배수의 개수를 빼는 과정이라 볼 수 있다. 그리고 실제 N에도 이 소인수들을 제거해야 하니까(ex. 12 = 2^2 x 3, 여기서 2^2를 제거) 반복문으로 나누어 준다. 그러면 for문의 (int) sqrt(N)에도 바뀐 값이 반영된다. 이렇게 되면 k는 3인데 1 < sqrt(3) < 2 이므로 반복문에서 빠져 나오게 되고, 남은 공약수(3)를 빼 먹게 된다. 그렇기 때문에 N이 아직 1 이상일 때는 N의 배수를 한번 더 제거함으로써(result -= result / n) 최종 result에 반영할 수 있게 한다.

'하나의 result 변수를 두고 거기서 또 추가적인 배수의 개수를 뺀다'는 과정을 살펴보면, 중복되는 배수는 이미 이전에 제거된다는 과정이 포함된다. 아까 12를 예시로 들었을 때 마지막으로 result -= result / 3을 하면서 이렇게 4 = 6 - (6 / 3) 계산해야 했는데, 1부터 12까지의 3의 배수를 2개(3, 9)로 볼 수 있었던 이유는 이전에 2에서 제거할 때 미리 빼줬었기 때문이다. 그래서 다른 거 생각할 거 없이 그냥 현재 배열의 값, 현재 변수의 값을 P[i] = P[i] - (P[i] / K), result = result - (result / k) 그대로 사용해 주면 된다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class BOJ11689 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
long n = Long.parseLong(br.readLine());
long result = n;
for (int k = 2; k <= (int) Math.sqrt(n); k++) {
if (n % k == 0) {
result -= (result / k);
while (n % k == 0) { // n에서 소인수 k(제곱) 삭제
n /= k;
}
}
}
if (n > 1) {
result -= (result / n);
}
System.out.println(result);
}
}
https://www.acmicpc.net/problem/11689
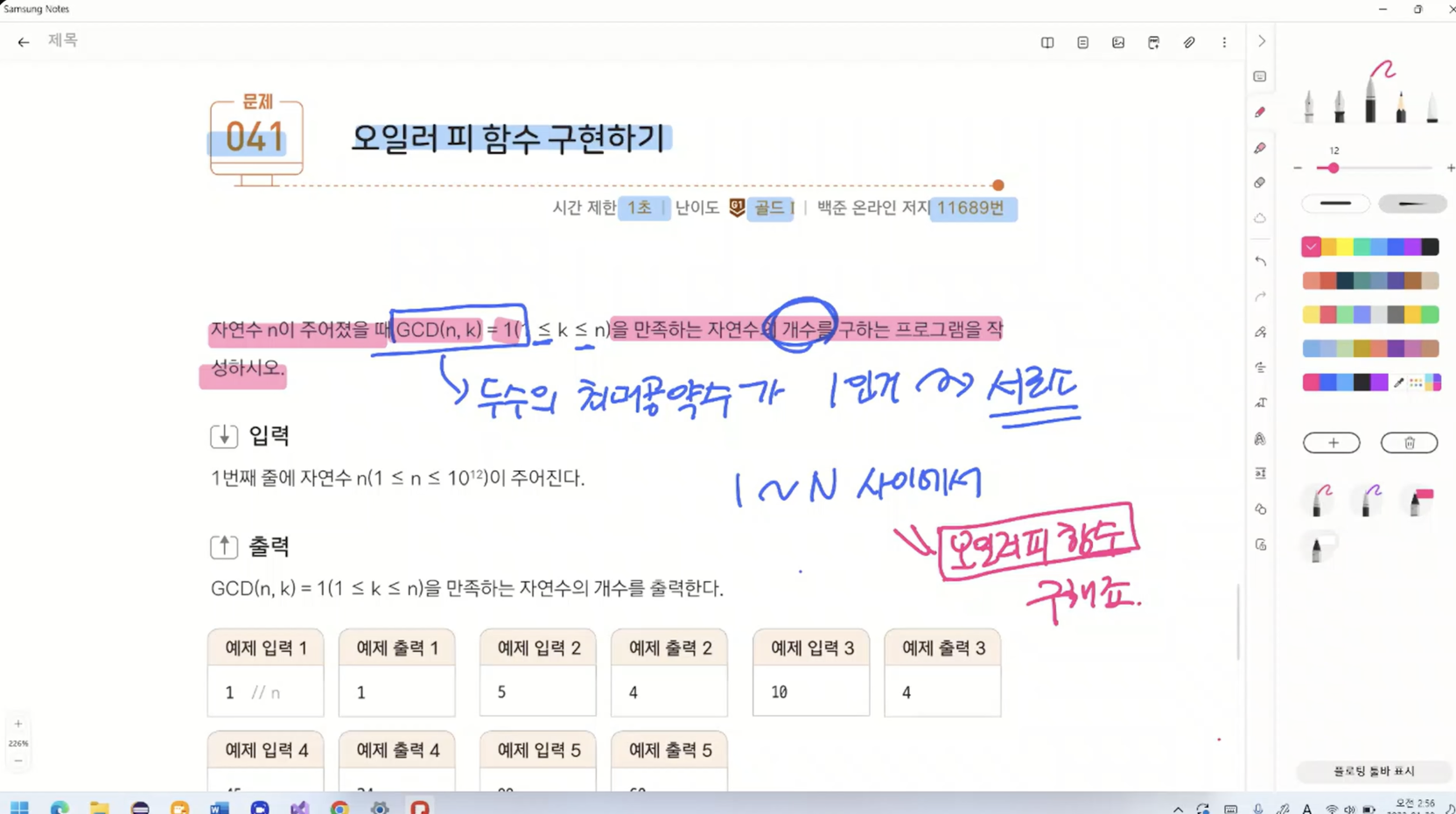
오일러 피 함수를 적용하면 쉽게 풀 수 있는 문제다.
'문제 및 이론 정리 > 코딩 테스트' 카테고리의 다른 글
| [코딩테스트] 확장 유클리드 호제법 접근 방법 (1) | 2024.11.28 |
|---|---|
| [코딩테스트] 모듈러(%) 분배 법칙 (0) | 2024.11.18 |
| [코딩테스트] 구간 합, 조합 (0) | 2024.07.08 |
| [코딩테스트] 호제법, 소인수분해, 에라토스테네스의 체(소수 구하기) - 정수론 (0) | 2024.07.02 |